方程中的隐秘暗影
纵观计算数学可视化的历史，方程绘图始终采用二进制模式——图表仅显示方程精确相等的区域。然而当视野仅限于黑白两色时，某些事物便隐而不显。在“误差==0”的表象之下，数学阴影始终潜伏于方程之中
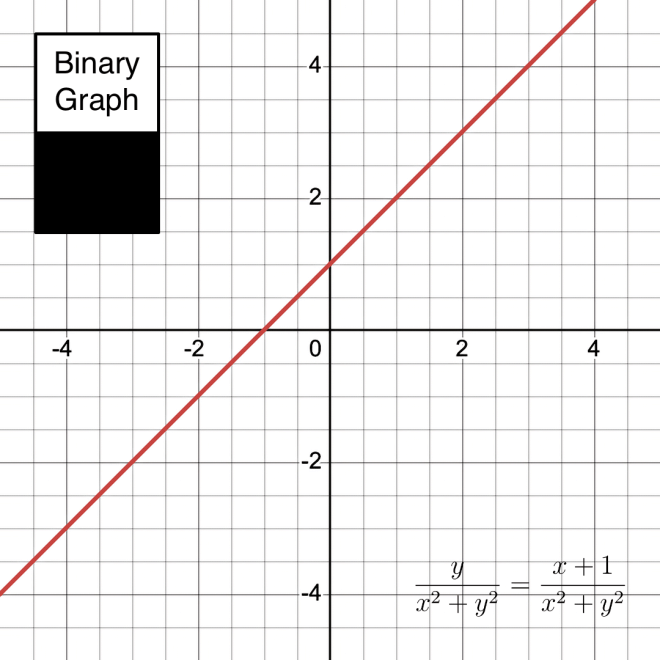纵观计算数学可视化的历史，方程绘图始终采用二进制模式——图表仅显示方程精确相等的区域。然而当视野仅限于黑白两色时，某些事物便隐而不显。在“误差==0”的表象之下，数学阴影始终潜伏于方程之中。
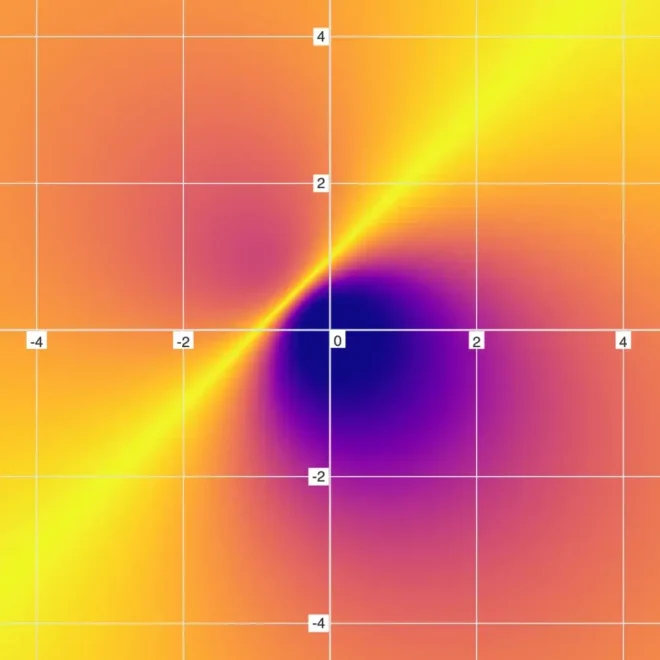
而FuzzyGraph采用非二进制模式可视化方程——不仅呈现精确相等的区域，更揭示近似相等与相差甚远(误差较高)的区域。有时这些高误差区域会形成清晰的视觉阴影特征。
让我们通过实例来观察…
实例1：斜点方程§
以下是“斜点”方程(1)的传统与模糊图形对比…
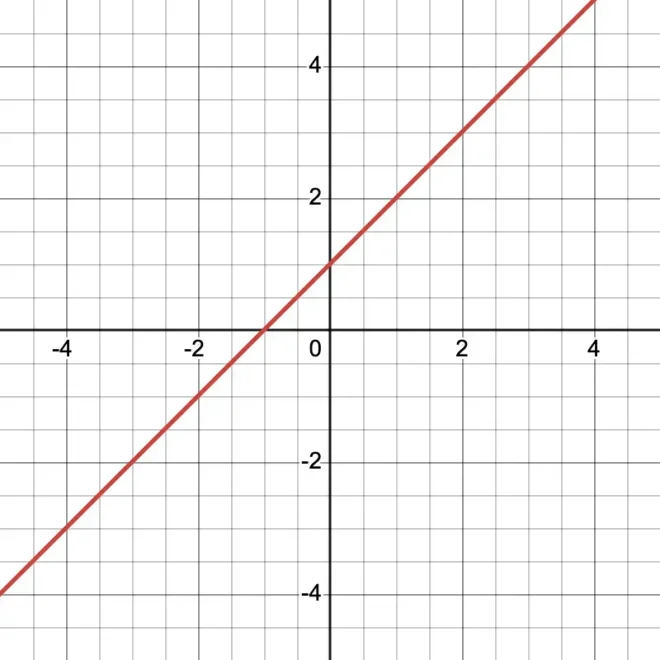
传统图示2
模糊图示3
注意模糊/非二进制图中存在的巨大黑洞区域，该区域在常规/二进制图中不可见。此“黑洞”特征代表方程中高误差区域。
示例2：类星体方程§
再看另一个示例：4
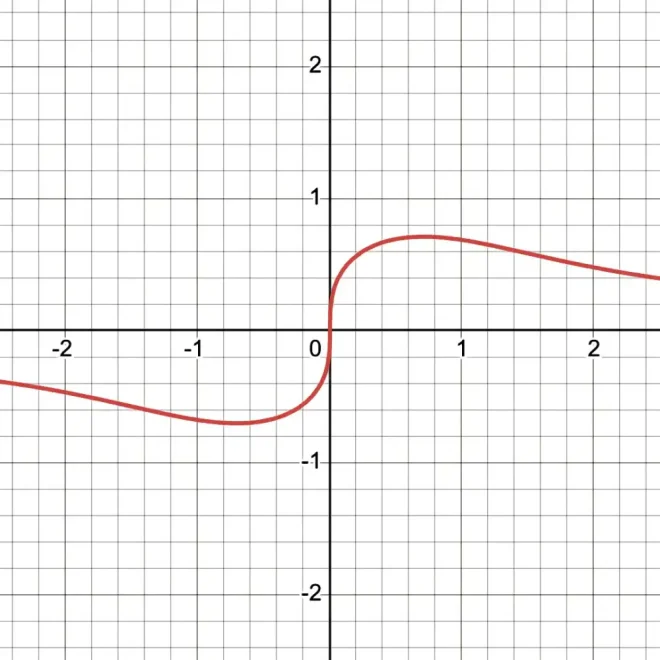
传统图示5
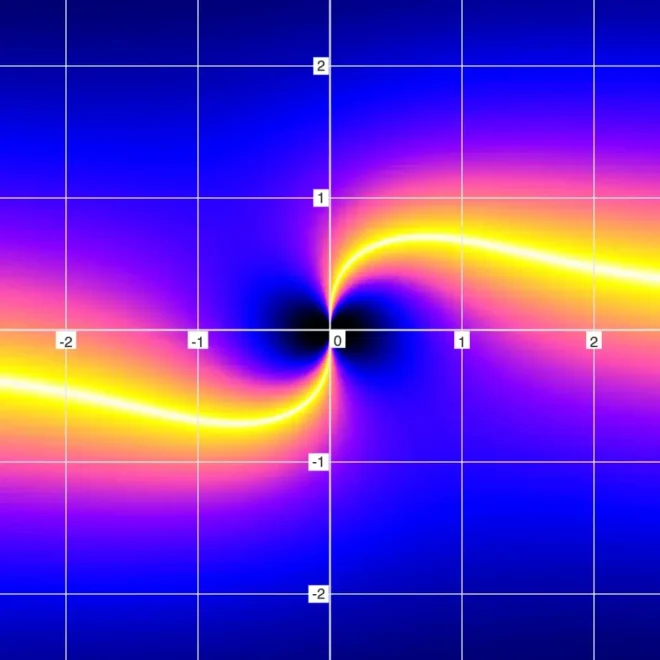
模糊图示6
请注意，在常规/二进制绘图模式下，黑洞的“眼睛”特征完全不可见。
示例3：简单恒星与黑洞§
为更清晰理解黑洞现象，我们通过简化示例说明。首先观察黑洞的对立面——简单恒星/粒子模型：7。该方程仅存在一个解：(0, 0)。若在常规绘图软件中绘制此图，仅会显示(0, 0)处的单点。但在FuzzyGraph中，它呈现为模糊粒子般的形态。
传统绘制的8图
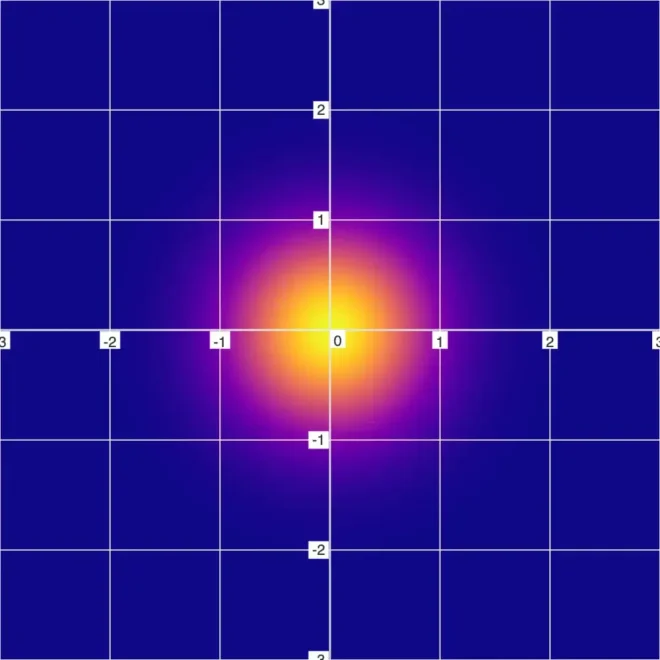
模糊图示 9
现在将此图反转即可得到“黑洞方程”：10…
常规图示11
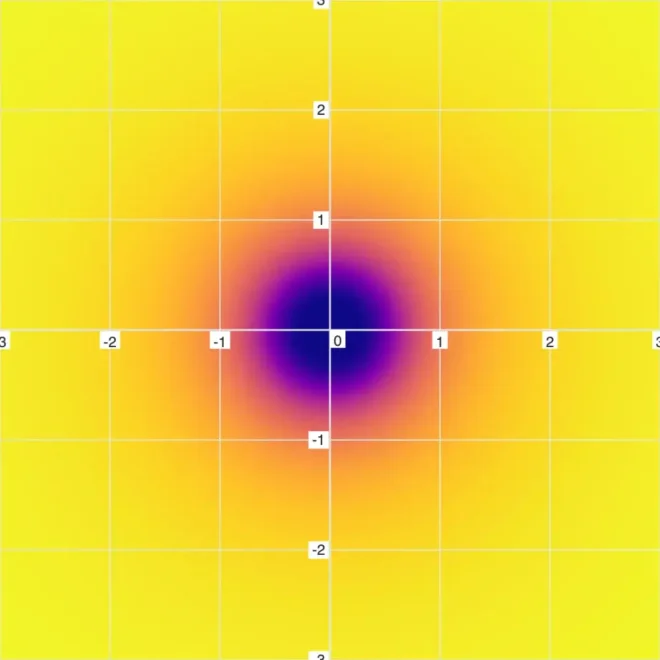
模糊图示12
此类方程存在实际解，传统图示完全无法呈现。但仍可通过数学拓扑学实现可视化(如模糊图所示)。
示例4：暗线§
并非所有暗线都如黑洞般存在。
本例中，我们先将两条线13与14合并。
通过将两个方程重构为等于0的形式，再相乘即可实现视觉上的相加。15可改写为16，17可重构为18。
随后将两者合并为单一方程：19
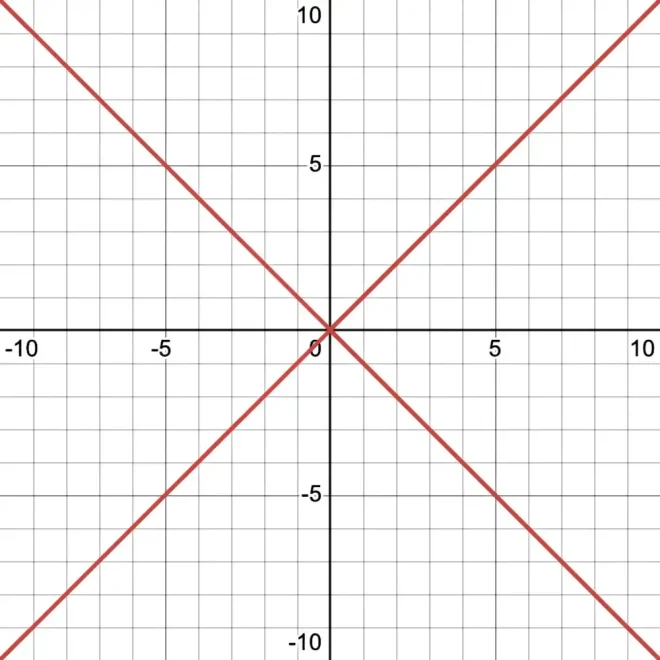
20的图形表示
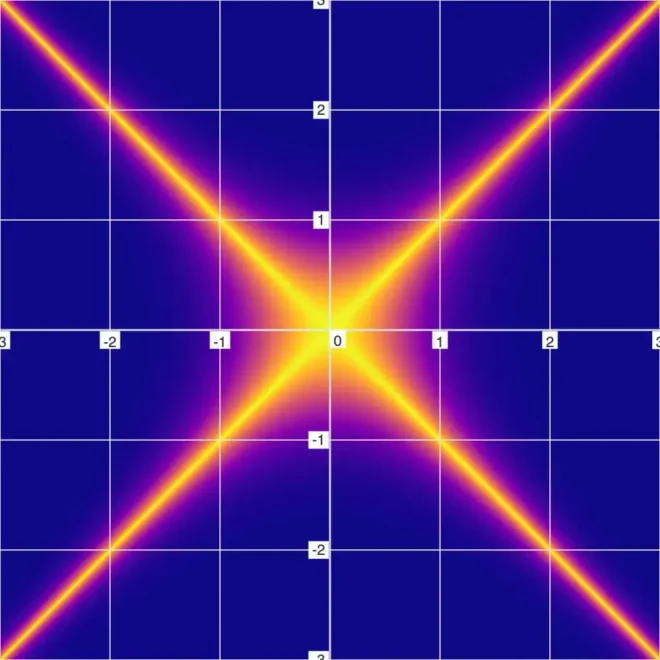
模糊图21
现在，我们通过除法对其中一个方程进行求逆：22
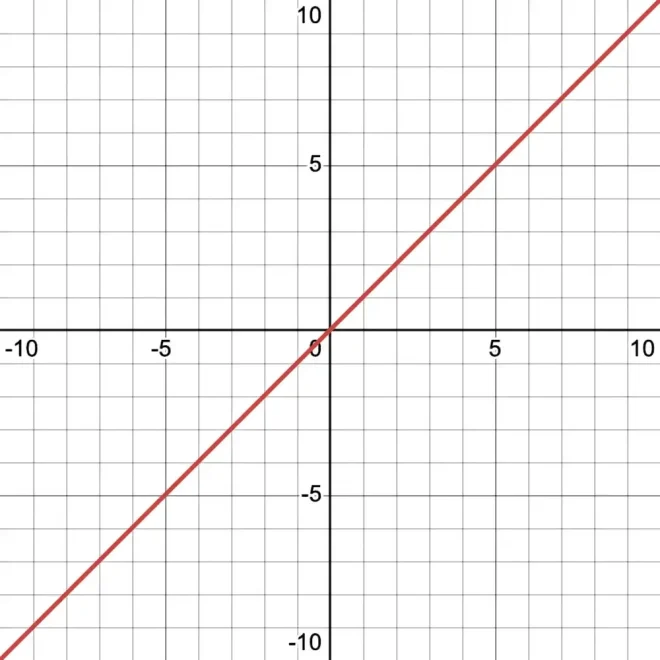
23的图形
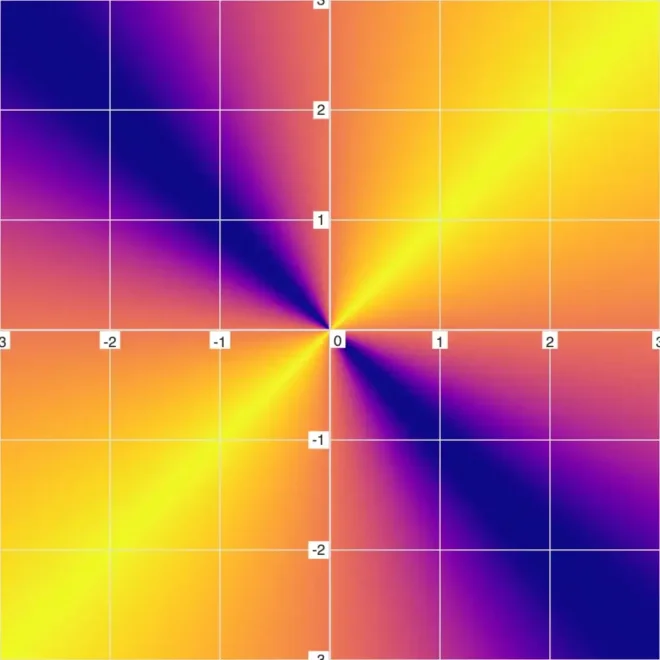
24的模糊图形
由此可见，被反转的线段(位于除法线下方)现已成为阴影线。相较于传统图形(其形态与更简单的方程25无法区分)，这种呈现方式似乎更符合视觉化需求。
示例5：菲方程§
该方程与前例原理完全一致。同样从乘法开始合并两个方程(此处为圆方程与垂直线方程)：26。
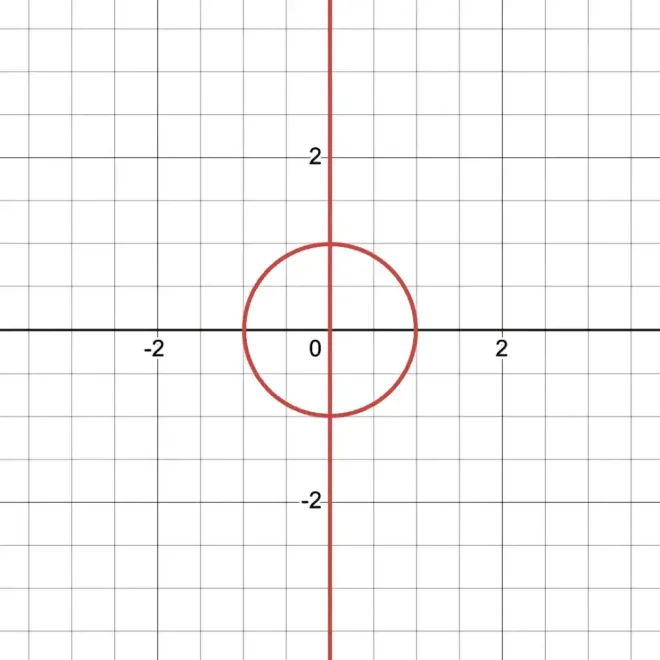
27的图形
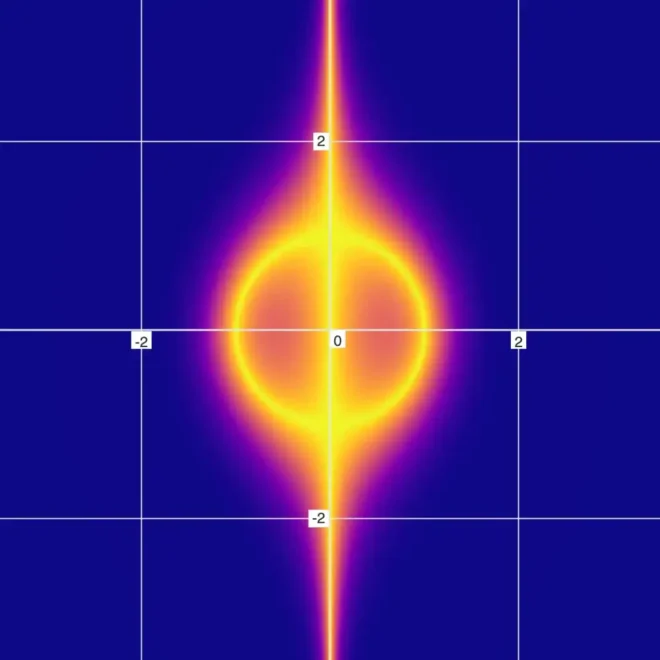
28的模糊图形
现在，我们通过除法将圆方程逆转，得到方程：29。
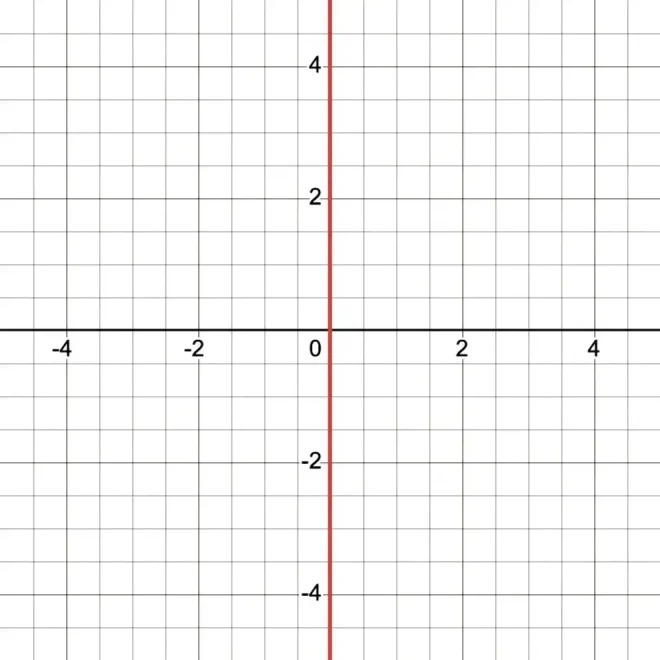
30的图示
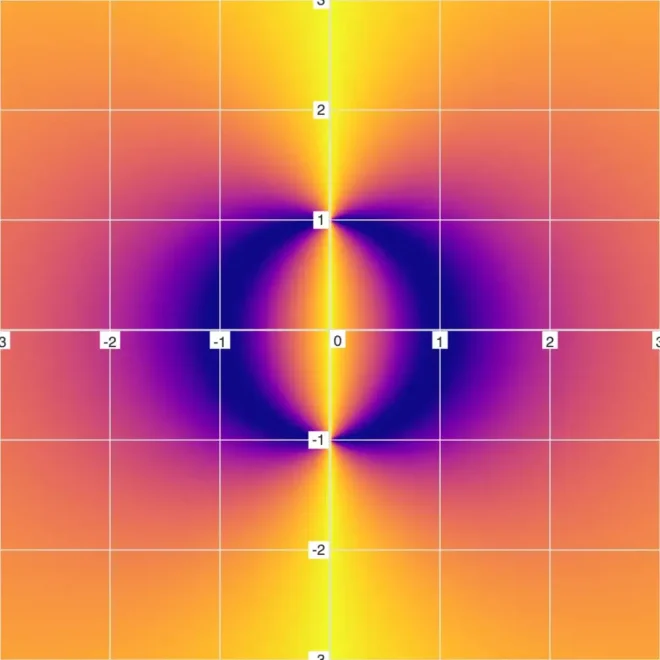
模糊图31
需注意，传统图形中阴影圆不可见。实际上，传统图形与32方程的传统图形完全相同(仿佛分母不存在)。
例6：水下岛屿§
在前文所有示例中，“阴影区”均代表高误差区域。但本例将揭示隐藏细节——低误差区域，这些区域几乎是方程的解。
请同时观察方程33的常规图与模糊图：
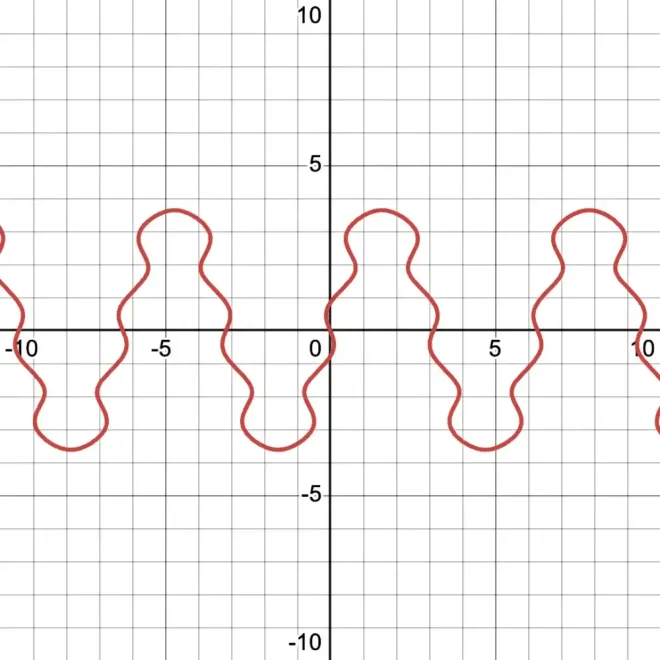
34的传统图形
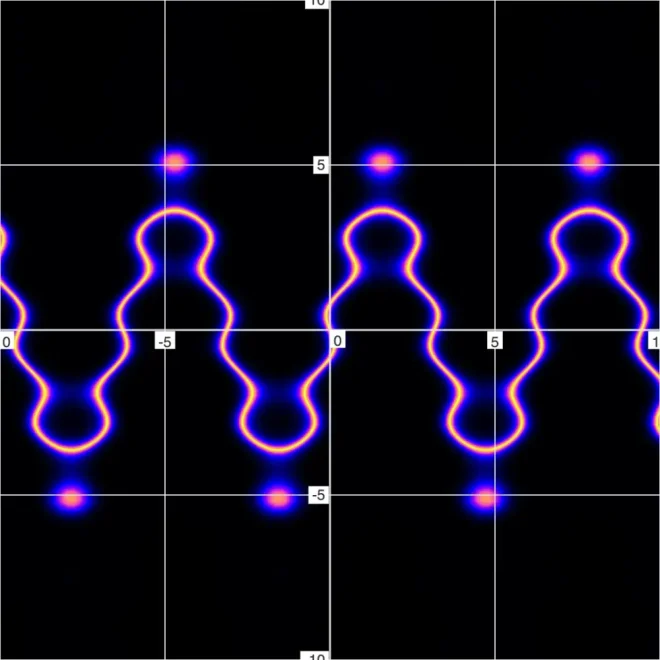
模糊图35
注意模糊图中出现的漂浮点，这些在常规/二进制图中并不存在。它们如同水下岛屿——位于水面(或本例中的36表面)下方的水下山脉。这些隐形岛屿代表方程的近似解区域(仅在模糊图中可见)。
它们的存在暗示着：若微调方程参数，这些区域便会破水而出(届时在常规图中也应可见)。
因此我们将方程从：
37 改为：
38…
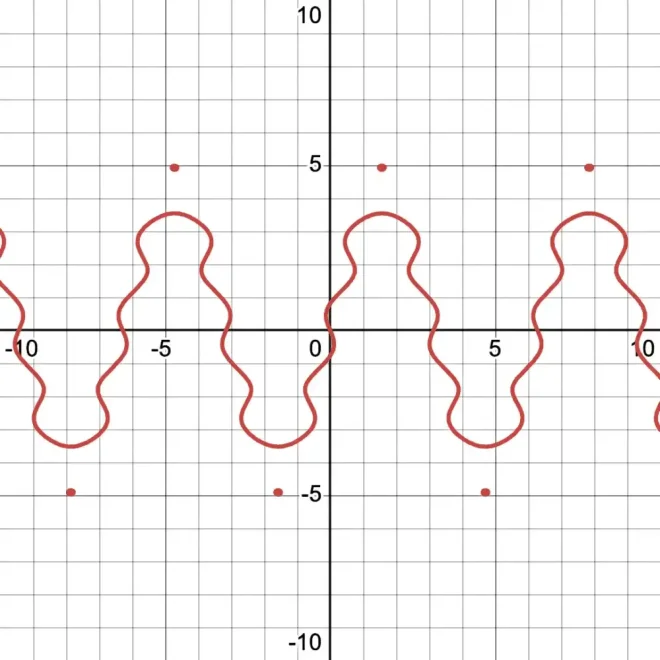
传统图形39
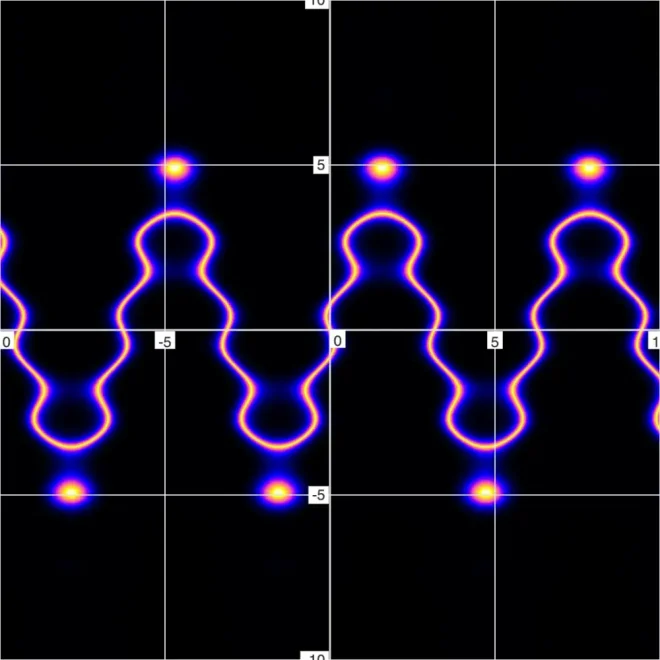
模糊图的40
如您所见，那些先前隐藏的岛屿现在在常规图中已清晰可见。
因此模糊/非二元图法能帮助我们洞察数学地形特征，这些特征在常规/二元图法下完全不可见。
本文文字及图片出自 The Shadows Lurking in the Equations，由 WebHek 分享。
设计精巧，但网站宣称这是“新型图形”的说法具有误导性[1]。F(x, y) = 0的模糊图本质上是z = |F(x, y)|的3D图，其中z通过颜色呈现。换言之，F(x, y) 构成约束条件，z 则反映约束被违反的程度。而 F(x, y) = 0 所呈现的图形，本质上是三维图形的截面。若宣称发现了用色彩可视化三维图形的创新方法，恐怕要晚了五十年。
[1] https://gods.art/fuzzy_graphs.html
我也有同感，因此将示例编程到Desmos 3D中(点击左侧的显示/隐藏按钮)。
https://www.desmos.com/3d/3divdux6jh
去掉绝对值后可获得更佳可视化效果。示例4“阴影线”的3D图具有确立名称——双曲抛物面。示例5“Phi方程”的彩色图未能体现奇异对称性F(x,y)=-F(-x,y)。示例6“水下岛屿”的彩色图远逊于3D曲面图。
有趣。我不知道Desmos能这样绘图。感谢你费心将它们输入。
不客气。虽然模糊图形作为等高线图已存在很久，我仍鼓励你多做尝试。这些颜色看起来很漂亮。:)
有个建议：计算z=left-right时去掉绝对值，尝试将[负极限, 0, 正极限]映射为[黑, 红, 白]，或将[负极限, 0, 正极限, 极限外]映射为[红, 白, 蓝, 黑]。当然，多尝试变体，享受创作乐趣！
这个方法我还没尝试过——或许不错。其实我一直在探索各种可视化形式，大部分作品都是用独立的Python脚本实现的。这里有个开源项目可作为Python数学艺术创作的起点：https://github.com/calebmadrigal/truthygraph.py。不妨亲自尝试你的创意 🙂
感谢各位反馈(无论赞同或反对)。Reddit确实是向聪明人展示想法的绝佳平台。
开篇或许有些夸张，我会考虑调整措辞。确实存在非二元化可视化误差梯度(机器学习领域)的案例，将三维空间映射为色彩(及三维图形)也并非创新之举。
但用“两边差异程度如何？”取代“两边是否完全相等——是或否？”来可视化方程，我认为是全新的思考方式——除https://fuzzygraph.com外，我尚未见过其他绘图软件/计算器实现这种功能。
有人或许会质疑：方程的“模糊图形”并非真实图形，因为其中施加了“可视化转换”，唯有传统二元图形才是方程的有效图形。但即便是传统绘图应用也必须对方程进行“可视化变换”——类似这样的逻辑：若Boolean(左(x, y)==右(x, y))则'黑'，否则'白'。
没错，开篇那句很容易被反驳。这会让“数学底子更扎实”的人产生怀疑。
除此之外…根据这里的讨论，这个绘图方式显然很有吸引力。对初次接触者而言，这是全新的思考方式。对于依赖标准绘图软件可视化方程的人来说，这很可能是一种全新的“绘图类型”。
或许可以强调它基于“比现有绘图软件更高级的数学原理”。这样既保持震撼感又基本属实。可以引用“隐函数定理”等酷炫数学概念——这些正是目标受众难以自行发现的知识点。
> 设计精巧，但存在误导性
您的评论颇具洞见，但措辞选择欠妥(这在我们这里恐怕也常有发生)。我完全不认为作者有意误导。
有时人们只是重新发明了轮子(或对其进行了改进)。若能借此向数千人传授新的可视化技术，我认为这终究是积极的。
你说得对，但作者开篇的论断刺痛了我的眼睛(我研究几何学)……作者似乎只是在绘制隐式函数y-f(x,y)的数值曲线……
所以，他做得不错，但提出如此宏大的论断时需要历史视角。
已知悉。
“纵观计算数学可视化的历史，方程绘图始终采用二进制模式…”
无论有意无意，该文开篇便抛出一个荒谬可笑的论断——由于其可验证的虚假性，甚至无法被当作夸大其词来宽容。每当我遇到此类故作高深的表述(通常出自初级工程师或刚毕业的产品经理之手)，我都会明确指出这类错误陈述如何严重损害论点本身。
这不仅令读者反感，更是毫无必要的。
“您可能习惯看到这样的图表…”或“小学时我们学过这样的绘图方法…”
这类表述或许比否定隐式函数可视化历史更有价值。希望下次作者能少些夸夸其谈。
读者可在此处尝试三维与二维绘制：
https://c3d.libretexts.org/CalcPlot3D/index.html
https://www.desmos.com/3d
但有些真相值得展示：
1. 这种绘图方式能显示 近似解 区域，这点 非常酷 。
2. 虽未提及，但它同时呈现了解周围的梯度分布，有助于直观理解吸引子/排斥子。
我之前确实生成过这类图来可视化误差或敏感性，但这次的呈现更简洁且酷炫。因此，传播这个想法的人值得赞誉。
我想知道是否存在拓扑工具能从该曲面中找到自交超平面——这实际上是方程的解？或者给定模糊图 z=|F(x,y)|，能否用微分几何找到 0=F(x,y)？这些问题有意义吗？
对于一般函数F，求解满足F(x,y)=0的点(x,y)并无闭式解法。整个数学优化领域主要致力于以各种形式求解F(x,y)=0的解。
当F具有特殊结构(如低阶多项式)时，我们能求得精确解。更一般的结构(如凸性、可微性)虽无法直接给出精确解，但可借助巧妙的数值算法求解。当F几乎没有结构时，可采用“黑箱”方法，这类技术在变量较少时效果尤佳。对于“模糊图”而言，仅存在两个变量，因此该软件采用计算屏幕每个像素点F(x, y)的策略。通常这会因维度诅咒而失效，但在低维空间中却能生成优质可视化效果 🙂
直接回答你的问题：是的，我们能运用微分几何加速优化过程。例如你可能听说过的梯度下降法。预条件梯度下降法正是利用曲面几何特性加速收敛。用微分几何术语表述：当优化函数 f(x) 时，x 是“反变量”而 grad(f) 是“协变量”，因此严格来说不能直接将 grad(f) 加到 x 上——它们类型不同。我们必须先将梯度与一个编码函数在x点附近局部曲率的二阶张量(即“预条件器”)相乘。Adam优化器正是采用此技术，其假设预条件器为对角张量。
学校教育习惯让你将函数视为显式形式 y = f(x)，但其实可以轻松转换为隐式形式 f(x) – y = 0，或更普遍的 f(x, y) = 0。由此可绘制 f(x, y) 的图形：既可作为三维曲面(f(x, y) 表示点 (x, y) 的高度)，也可将 (x, y) 处的函数值编码为该点的颜色。当曲面等于零时，即与 z = 0 平面相交处，这些点即为 y = f(x) 的解点。而 f(x, y) 值为小于零的非零值的点 (x, y)，正是文章所称的低误差点或区域——这些点或区域几乎满足 y = f(x)。
> f(x, y) = 0。由此可将f(x, y)的图形绘制为三维曲面，其中f(x, y)即为点(x, y)处的高度值
若f(x, y) = 0，使用f(x, y)作为高度值是否会导致图形呈现平面？
f ( x , y ) = 0 仅对 某些 x 与 y 的组合成立。这是待求解的方程，既非全称命题(如∀ x , y : f ( x , y ) = 0)，亦非定义(如 f ( x , y ) ≔ 0 或 “≝”)。该方程的解是使函数图像高度为零的点( x , y )。具体是哪几个点取决于 f 的定义方式。
例如， f 可定义为 f ( x , y ) ≔ x ² + y ² – 1。此时当 f ( x , y ) = 0 时，对应的点 ( x , y ) 位于单位圆上(即满足 x ² + y ² = 1 的点)。函数图像仅在这些点处高度为零。
这两种等号本质上属于不同类型。
f(x,y) = x+y 或许更适合写成 f(x,y) := x+y，其中 := 表示“定义为”。那么 f(x,y) = 0 就是一个方程，展开后为 x+y = 0，或用初等代数中常见的形式表示为 y=-x。
g(x,y) := 0 确实 就是 一个平面。
我虽在编程中见过 := 多年，却总以为它本质上就是 =。感谢您的解释！
需要说明的是，在编程中它通常用于赋值操作，这与定义的概念并不完全相同。Go语言用它声明变量，所以用法相当接近。
在此语境下，当我们说“f(x, y) = 0”时，通常还会单独给出f(x, y)的定义，且该函数值并非对所有x,y都等于0。因此约束条件“f(x, y) = 0”的含义是“找出使得f(x, y)等于0的x和y组合”。
若“f(x, y) = 0”本身即是f(x, y)的定义，那么确实会得到相当单调的图形。
自我宣传一下：八年前我创建了这个网站，用于展示采用类似梯度绘制的复函数图：https://kettenreihen.wordpress.com/
这些图确实赏心悦目。我总忍不住想点击它们了解更多，真希望有些能附带简短说明作为基础知识补充。
哎哟，读着真刺眼。这既不新颖，又缺乏最基础的数学认知。
根据定义，函数 y/(x^2+y^2)=(x+1)/(x^2+y^2) 的图像必然包含满足该方程的点集——这恰恰就是 y = x + 1 的解集。
所谓“模糊”图形只是标注了左侧与右侧的差异。这属于基础知识，毫无新意，更不可能是“y/(x^2+y^2)=(x+1)/(x^2+y^2)的图形”。
这让我很困惑——我脑子里也把分母消去了。
但后来我意识到他们只是绘制
y/(x^2+y^2) – (x+1)/(x^2+y^2) = c
并按c值着色(即热力图，正如帖中其他人提到的)。
这正是其图像比 y – (x + 1) = c 更具表现力的原因
为何说这不是 y/(x^2+y^2)=(x+1)/(x^2+y^2) 的图形？我认为传统/二元图同样不是方程的“纯粹”表现形式，而是一种可能的呈现方式——即通过“左侧 == 右侧？”布尔过滤器处理后的结果。事实上，任何不经处理的方程都无法直接可视化。
方程中存在等号，这意味着当y=x+1时成立。我们并未施加任何过滤，这正是方程本身的表述。你绘制的实为f(x,y)=(y-x-1)/(x^2+y^2)。当该值等于零时形成线性图，模糊图则对应其余情形。但请注意：f(x,y)=0 与 y=x+1 完全等价。两者本质相同。因此绘制模糊图时，你绝对不是在绘制 y=x+1 的图像，而是绘制 z=(y-x-1)/(x^2+y^2) 的图像——这两者截然不同。
若我们从 z(x,y) 开始，才需要“应用滤波器”得到直线图，但你写的内容并非如此
我认为楼主基本察觉到你并非专业数学背景，正试图用初中数学课本来解释。
“函数图”最简单的定义是：满足某个基础等式的一组点。你的图并非如此。更常规的名称应是热力图：它绘制的是一个接收两个参数(x和y坐标)的函数，并为每个坐标赋予第三个值(颜色)。
我认为这种区分并不重要。它们本质上都是函数图。
函数的“图像”在形式上被精确定义为使方程成立的点集。https://en.wikipedia.org/wiki/Graph_of_a_function诚然，图像只是函数的一种 可视化呈现 ，并非唯一有价值的形式。
当然我们还需谨记：函数不等同于方程，同一个函数(或更普遍的映射关系)可由多个不同方程表示。举个简单的例子：将slashdot方程两边乘以常数，或添加x*y项。
这是方程误差面的热力图…在优化与梯度下降领域，这个概念已被相当深入地理解。
有趣的是，图中呈现的其实是未知方程的失效模式——误差为零的谷地，导致所有解都成立。若误差测量引入噪声，谷底过于平坦便会引发异常行为。
喜欢这类图表的人，或许也会对复函数的定义域着色图感兴趣：
https://web.archive.org/web/20120208174423/https://maa.org/p…
https://observablehq.com/@rreusser/complex-function-plotter
事后看来这既精妙又显而易见。可测量的价值几乎总伴随噪声，方程解也极少趋近真实零值。设置微小误差是常规做法，但这些图表揭示某些方程在此操作下可能产生异常行为。
进一步推演：若用此视角审视简单算法，它们将呈现何种行为？我们不仅能观察结果，更能窥见可能性空间…
迈克尔·莱文曾探讨过冒泡排序算法的有趣动态——这段仅几行代码的程序竟与生物过程存在平行关系，暗示自然界存在着我们尚未察觉的更微妙逻辑。
这听起来很像神经网络编码的程序。
这不就是用高级语言实现的吗？调整算法允许重复项，然后惊讶地发现存在聚类现象？
我的意思是，我不明白这有什么特别之处？若我理解有误请指正。我欣赏他关于生物电空间的研究观点，但这点我确实没看懂。
聚类现象不值得惊讶？你是说这是高级表征的伪像？特殊性——或许本身不算，但当单细胞生物也展现相同策略时，至少耐人寻味。
系统随机为细胞分配类型。某些细胞若左侧数值较大则向左移动，另一些若右侧数值较小则向右移动，还有些随机往返移动。
我不明白为何你会惊讶于最终未形成完全排序却仍存在聚类现象。
这完全符合我天真的预期。
这确实赏心悦目，但不就是取第一个方程减去第二个方程的绝对值吗？这些可视化效果固然精美——但将其包装成某种“视角的颠覆性变革”似乎毫无意义。
太酷了！这在计算机图形学中称为有符号距离函数，数学领域则称作隐式方程。
这是无符号距离函数；应为|f(x)-g(x)|而非f(x)-g(x)。传统线性图才是由方程隐式定义的图形。
模糊图(即文章展示的图表)的原理是：将每个点代入公式(方程)后，观察其偏差程度。重大偏差→暗区(如苦涩滋味)。微小偏差→亮区(近乎正确)。它仅呈现代入x和y后产生的原始误差。
采用有符号距离函数时，我们不再关注公式误差，而是测量点距完美曲线的距离——如同取出直尺测量至“正确”直线的最近距离。
该函数始终具有长度单位，且行为良好(曲线外侧为正值，内侧为负值，曲线上为零值)。
因此模糊图展示的是“方程在此处的偏差程度”
而有符号距离函数则体现“与精确解的距离远近”
二者理念相关(均源于形如“某项=0”的方程)，但本质不同。
我合理地自问：“难道暗区不代表远距离，亮区代表近距离吗？”
深入思考后：
在模糊图中，我们根据方程误差着色——即方程在每个点满足程度的偏差。
而在有符号距离场中，我们根据实际几何距离到曲线的远近着色。
除非方程以非常特殊的方式书写，否则这两个数值并不相同。若将方程乘以巨大系数(例如所有项乘以1000或除以极小数值)，解曲线的形状不会改变——距离未变——但方程误差会骤然扩大(或缩小)1000倍。这将彻底改变模糊图的阴影分布，而实际距离却毫无变化。
有符号距离是通过直尺测量(纯几何学)。模糊图则测量代数误差(公式接近零的程度)。两者在曲线附近都可能变浅，远离曲线时变深，但成因不同，因此不可互换。
我花了一会儿才理解这些图表的含义，因为我通常将曲线拟合到数据上。所谓“低误差”区域，是指若存在数据点，其置信区间会很宽的区域——即置信度低且模型更可能存在高误差的区域。
图中暗色区域似乎是决定曲线形态的关键特征。这意味着这些区域应是绘图器最确信的部分，否则曲线形态将发生变化。而明亮的“低误差”区域则表明模型在此处最可能出现偏差。
或许存在更合理的解释，但我认为“误差”在此处的用词可能不妥。它不仅表示“A与B的差异”，更包含某种“错误程度”的衡量概念。
我一直称之为“误差”(方程左右两侧的差值)。但若有更恰当的术语，我希望能了解。
我认为“差值”更合适，因为“误差”暗示一方正确而另一方是近似值。具体来说，你绘制的是绝对差值 z = |f(x, y)-g(x, y)|(更糟的是绝对误差)，而非误差。
太棒了！
多年前我曾制作过复数域着色在线演示，与这个想法相关：
https://anematode.github.io/grapheme-math/demo/domain_colori…
我第一反应是“如何在3D环境中实现并用VR漫游？”
VR部分我能实现——能否分享算法？这样我就能让机器生成立体效果。我认为三维图形工具需要空间化处理才能充分展现其价值。
只需将两个函数相减，取绝对值，再通过色彩渐变映射即可。若想在3D中呈现，可将函数差值输入三维图形绘图器。构建三维曲面绘图仪才是难点，但现有设备可直接使用，例如将公式“abs(y/(x^2+y^2) – (x+1)/(x^2+y^2))”输入此处：
https://c3d.libretexts.org/CalcPlot3D/index.htmlT
该查看器还具备“2D”模式，可生成彩色二维图。
问题在于，我更像工程师而非数学家，虽然明白这完全可解，但从零构建可能导致大量错误且缺乏乐趣。
三维图虽美却称不上“空间化”——毕竟仍是平面渲染，而我真正关注的是物体的网格化处理。我熟悉德劳内和行进立方体策略，至少能让机器将其连接到空间绘图仪上
Desmos也有不错的渲染器：
https://www.desmos.com/3d
能否用混沌函数运行这个模型？我很想看看会产生什么图案。目前尚未找到生成此类图案的代码或模型。
类似于复平面映射中 z = f(z') 的关系，即复平面中某点的新的 z 值是该点当前 z 值的函数。
虽然这种视角有其价值，但受限于所有示例均采用极坐标方程，导致图示效果过于夸张。考虑到极坐标关系的笛卡尔表示始终是底层圆锥曲线的平面投影，在有效点附近出现极值点实属正常。
若能直观展示线性关系将更有意义，但显然其中的误差无法构成如此引人注目的博文素材。
这似乎是同时可视化多个密切相关方程解集的一种方法。我好奇若不按误差着色，而是将所有解集按系数取值范围进行复合，图形会呈现何种形态。
我不敢说理解“误差=0表面”的计算方法(他们解释过吗？)。
但好奇这些图表能否/是否通过真实数据经验验证过。
推测他们只是将方程左右两侧的绝对误差渲染到图表每个像素点。
没错——就是|左值-右值|^模糊度
他说明模糊化如何定义了吗？
我需要补充细节。但本质上就是：abs(左值-右值)^模糊值
> 这种情况下传统图形完全无法显示，因为方程存在实际解。
感觉这里少个“不”字，不过我数学差，说不定没问题。
没想到居然有Slashdot方程，真意外。:)
这不就是分形着色的原理吗？
原理相似，但多数分形中，着色数字代表达到特定阈值所需的迭代次数(该阈值标志着分形开始发散)。
没错，我的意思是除了等式之外，你还可以绘制更多内容来实现可视化。我认为这也是可视化博弈论内容的常见方式。你既想知道预期均衡点的位置，也想本质上了解达到该均衡点的可能性强度。
真是美妙绝伦。我敢说拉马努金当年就是这样“看见”并感受到这些的。
真希望绘图工具能支持径向模式，肯定能呈现超酷的对称效果。
这不正是数学家们用“等高线”做的事吗？
自1960年代起，科学家们也用此法可视化偏微分方程解。作者不妨下载Paraview软件尝试旋转视角，就能获得这种效果。
首先创建网格(来源->平面用于2D，或来源->盒子用于3D)。将该源的分辨率设置为较高数值。接着使用滤波器应用函数：简单运算可选滤波器->按字母排序->计算器，复杂运算则选滤波器->按字母排序->Python计算器。“coordsX”等参数代表网格上的空间坐标。可自由选择颜色映射(发散型映射效果较佳)，调整着色范围，使用对数刻度等。
若在三维盒体中操作，可通过切片在任意倾斜平面上滑动查看结果。既可可视化恒定“误差”的半透明等值面并进行光线追踪，也可计算“误差”梯度绘制矢量场。稍加处理即可添加第四维度(时间)生成动画。所有这些方法皆可组合运用，可能性无穷无尽。
我近期了解到https://en.wikipedia.org/wiki/Level_set概念，其原理与此高度相似。
这类方法在90年代图像处理领域很流行：例如https://shape.polymtl.ca/lombaert/levelset/
老兄，学习新知识甚至撰文分享都无可厚非。但若连水平集这类基础概念仍在摸索，或许该暂缓宣称自己发现了数学发展数百年后全新的绘图形式？
作者确实用了夸张手法。身为艺术家，我认为这很正常。我个人觉得这种夸张的艺术表达并无冒犯之意
若能省去嘲讽作者不懂等高线知识的部分，你的批评会更有说服力
这种非建设性的侮辱掩盖了你对作者夸张手法的合理(尽管有些夸张)批评，去掉这种语气会更好
> 老兄，学习新知识甚至撰文分享都无可厚非。
关于等高线的核心问题在于：作者不仅缺乏论证创新性的专业背景， 他们明明掌握着所有必要线索 却未能意识到自身知识的匮乏。
这更像是玄学而非严肃的创新主张，别太较真。
> 一种名为“模糊图形化”的新型绘图技术
> 在计算数学可视化的整个历史中，方程绘图始终采用二进制模式
这些都是非常具体、非神秘主义的主张。但你真觉得“神秘主义”更适合这里？
“首个支持输入隐曲线并生成其等高线图的应用”与“计算数学可视化史上，方程绘制始终采用二进制模式”是截然不同的主张。
80年代装饰墙壁的数百万张绚丽分形海报，正是你论点的鲜明反例。
你的应用很酷，可视化效果也很棒。但那些夸张的原创性宣称实在有损其价值。
公平地说，确实存在非二进制绘图的应用场景(如人工智能中的误差梯度图)，但据我所知，这是首个能输入基础x/y方程即可生成非二进制图形的应用。
呃…你不过是把两个变量的函数(R^2 → R)画成了热力图。
“需注意，传统图形中阴影圆不可见。事实上，传统图形与x=0方程的常规图形完全一致(仿佛分母不存在)。”
呃… 没错，因为方程 x / (x^2 + y^2 – 1) = 0 简化后等于 x = 0。你的“模糊图”实际上只是函数 z(x, y) = |x / (x^2 + y^2 – 1)| 的绘图，其中 z 被编码为颜色。
反复阅读并沉淀后，我仍感到不安。
这种表达似乎更易造成干扰而非澄清。例如类星体方程。我不明白大写字母M的含义——在(X, Y)=0处，是否存在y与x/(x^2+y^2)差异更显著的区域？
但反驳自己：
我看的只是个玩具例子。
我确信自己曾多次真正 比较 过两个方程，需要理解它们的差异所在。
只是当其中一个方程是“y”时，我更难理解。
好吧，起初我还以为是些营销废话，但…它确实比传统黑白二分的图表提供了更多信息。
令人印象深刻。
计算机总在追求完美上浪费大量时间，其实“足够好”就能达到同样效果。若我们能更精准地定义“基本正确”的标准，就能通过牺牲精确度换取速度来加速软件开发。这种思路在量化LLM和JPEG压缩技术中已有体现。